Los sistemas de representación tienen como objetivo representar, sobre
una superficie bidimensional (como puede ser una hoja de papel), los objetos que
son tridimensionales en el espacio.
TIPOS DE PROYECCIÓN
Para representar objetos tridimensionales
en dos dimensiones recurrimos a su proyección en un plano (plano del cuadro o de proyección), mediante los rayos proyectantes.
El tipo de proyección determina el tipo de representación
o perspectiva.
- Proyección cilíndrica ortogonal: los rayos proyectantes
son todos paralelos y perpendiculares al plano de proyección. Este tipo de proyección es el que utilizamos en el sistema
diédrico, en el sistema de planos acotados y en las perspectivas
axonométricas ortogonales.
- Proyección cilíndrica oblicua: los rayos proyectantes son
todos paralelos y forman un ángulo oblícuo con el plano de proyección. Este sistema de
proyección es el utilizado en las perspectivas
axonométricas oblicuas (perspectiva caballera).
- Proyección central o cónica: los rayos proyectantes convergen (se juntan)
en un punto. Este tipo de proyección es el que utilizamos en la perspectiva
cónica.
TIPOS DE SISTEMAS
Perspectiva axonométrica
Dependiendo del ángulo que forman los tres ejes de referencia (x, z, y) con
el plano de proyección, hay tres tipos de perspectiva axonométrica:
- Isométrica, cuando los tres ejes forman el mismo ángulo (120º).
- Dimétrica, cuando sólo dos ejes forman el mismo ángulo (100º, 130º, 130º).
- Trimétrica, cuando los tres ejes forman tres ángulos distintos.
Perspectiva caballera
La anchura y la altura (y, z) del objeto, se proyectan en verdadera magnitud (sin distorsionar), mientras que la profundidad (x), se reduce a una proporción determinada, siendo los coeficientes de reducción más habituales: 1:2, 2:3 y 3:4. Otra diferencia con la perspectiva isométrica, son los ángulos: los eyes Z e Y forman un ángulo de 90º.
Perspectiva cónica
Hay dos tipos de perspectiva cónica:
- La central, cuyos rayos proyectantes convergen en un único punto de fuga.
- La oblicua, donde los rayos proyectantes convergen en dos puntos de fuga.
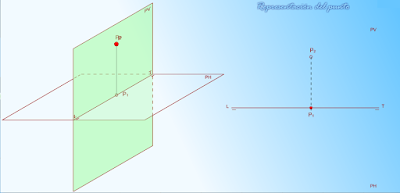
Sistema diédrico
Es un método de representación geométrica de un objeto tridimensional sobre un plano (un espacio bidimensional), es decir, la reducción de las tres dimensiones a las dos dimensiones, utilizando una proyección ortogonal
sobre dos planos (el plano vertical y el plano horizontal) que se cortan perpendicularmente. La recta en la que convergen se denomina línea de tierra.
El sistema formado
por los dos planos se denomina diedro, y se divide en cuatro cuadrantes numerados en el sentido contrario a las agujas del reloj. Para generar las vistas
diédricas, uno de los planos se abate sobre el segundo, permitiendo la
representación de las proyecciones del objeto en un plano.
———
MÁS INFO: